[ベスト] 三角形 角度 の 求め 方 283546

 図解でわかるその使い道と公式の証明｜アタリマエ！ 余弦定理とは何か？ 図解でわかるその使い道と公式の証明 とおいたときに、 以下の3つの式が成り立つことを余弦定理 と言います。 余弦定理は、「2辺の長さとその間の角度」から「残り1辺の長さ 円周角の求め方6 げっ、円周角じゃないとこきかれてるじゃん。 でも中心角を頂角にする三角形が「二等辺三角形」ってことを利用すると・・・ つまり50°の半分、25°が円周角だね。 二等辺三角形の底角は等しいからxも25°。 円周角の求め方2 補助線を引くパターン 次はちょっと難しい問題。 補助線を引かないと円周角が求められない やつだ。 円周角の問題7 さあ、補助線を引くぞ。正弦定理から，三角形の辺の長さを求める計算について ABCにおいてa = 3 ，A = 60°，B = 45°のときbを求めよ。 という問題がありますが， これを定理にあてはめていって， b = 3 / sin60°× sin45° まではつくれるんですが，そこから (3 ÷ √3/2 ) × 1/√2= 6/√6=√6 というのになるのが，意味がわかりま

角度を求める問題 スリッパを探そう 苦手な数学を簡単に

三角形 角度 の 求め 方

三角形 角度 の 求め 方-三角形の角度を求める 問 ABC A B C について， BC B C の中点を D D とすると， ∠DAC = 15°，∠ADB = 45° ∠ D A C = 15 ° ， ∠ A D B = 45 ° となった． ∠BAD ∠ B A D を求めよ． 16/8/ 幾何 ★★★☆☆ hide or visible 問題の説明 一見，シンプルな図形の問題に見えますが，なかなか手ごわいです．大学入試で問われてもおかしくありません．初等幾何のセンスを磨くにはちょうどよい問題 直角三角形の3辺 a、b、c 関数電卓の角度 前回 計算尺の使い方第6回 円の直径と面積 計算尺を使った対数の求め方 計算尺を使うと、10を底とする常用対数の小数部分である仮数を求めることができます。

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

 多角形（四角形・五角形・六角形・・・）の内角の和の公式＆問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されます。Cot (コタンジェント)から角度 ・ 三角関数の変換 三角関数を計算し変換します。 sin (サイン)を変換 cos (コサイン)を変換 tan (タンジェント)を変換 cos (コセカント)を変換 sec (セカント)を変換 cot (コタンジェント)を変換 三角形の計算 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか

なお、斜辺と高さから直角三角形の角度を求めていくには、三角関数であるsin（サイン）の逆関数sin1を使用します。 上述の三角形において、sinθ＝高さ/斜辺という関係式があるため、θ＝sin1（高さ/斜辺）で角度を求めることができるのです。 エクセルでは、 ASIN関数 というものを使用していきます。 ASIN関数でもラジアン表記であるため、度数法での記載に変更二等辺三角形の角度の求め方（計算） 色々な二等辺三角形の角度を求めましょう。下図をみてください。頂角が90度です。前述した計算式を使います。 α2θ＝180 902θ＝180 2θ＝90 θ＝45 頂角が直角の二等辺三角形を、直角二等辺三角形といいます。次の問題です。教え方1 三角形の3つの角の角度をたすと何度になるか考えさせます。 問い 三角形の紙を用意して、適当に手でちぎって3枚に分け、3つ角をくっつけるとどうなるでしょう？ 実際にやらせたあと、下の動画を、見せます。

 今回は、 三角形の角度を求める問題 を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ＝となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ こんな感じで別の解き方もあるよ！ まず右の三角形の内角の和180°を利用して、 ★1 を求める。 ★1 と ★2 は対頂角なので等しい; 座標計算の求め方 2点の座標値が器械点A (1749 7870)、視準点B (1801 )を計算する場合 直角三角形を作り、bとcの距離とθの角度を求めてみましょう。 bとcの距離は以下のようになります。 b =X2X1=5372 C =Y1Y2=997 次にθを求めてみましょう。

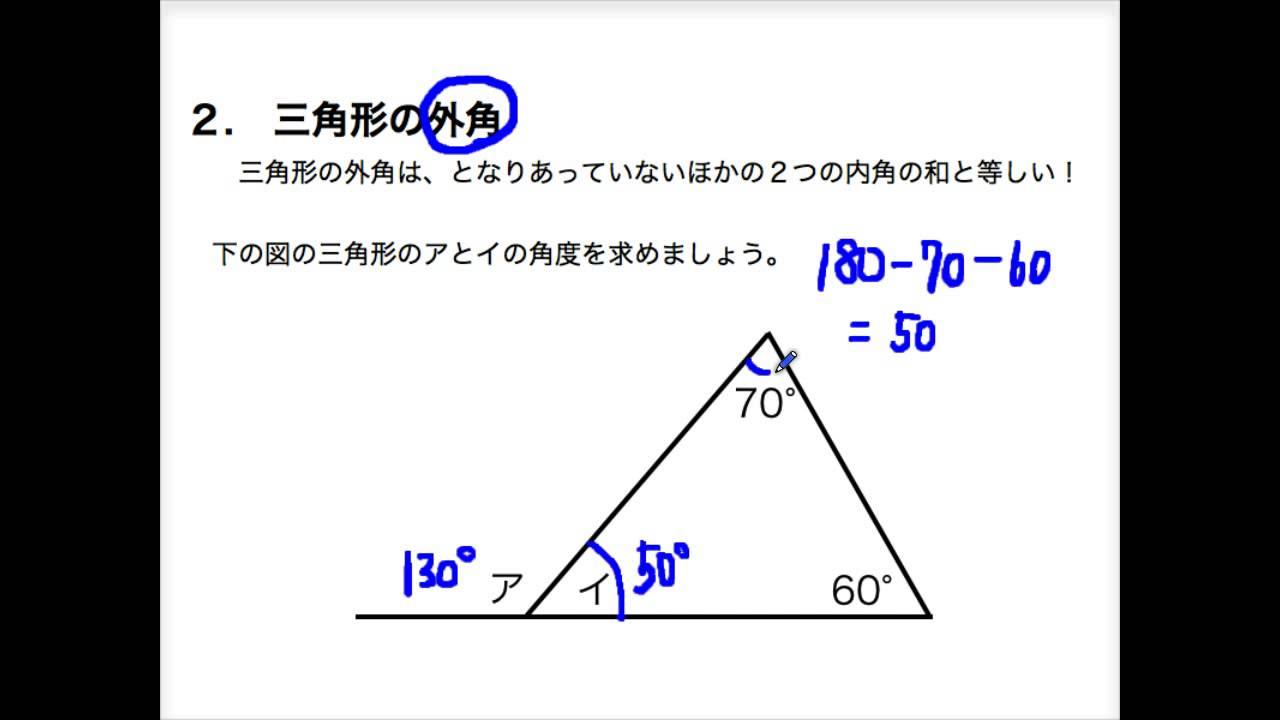
小学校5年 算数 三角形の外角 Youtube

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

 B c 2 = a 2 b 2 − 2 a b cos ⁡ C 余弦定理は三角比の中で出てくる 非常に有用な定理 です。 三角形の辺の長さや、角度を求めることができる からです。 今回はそんな余弦定理を使って、三角形の角度を求める方法を紹介していきたいと思います！ 求め方 （1）三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。三角形の計算 ・ 正三角形 (辺から高さと面積) ・ 正三角形 (高さから辺と面積) ・ 正三角形 (面積から辺と高さ) ・ 直角三角形 (底辺と高さ) ・ 直角三角形 (底辺と斜辺) ・ 直角三角形 (底辺と角度) ・ 直角三角形 (高さと斜辺) ・ 直角三角形 (高さと角度) ・ 直角三角形 (斜辺と角度) ・ 角度から三角関数 ・ 三角関数から角度 (逆三角関数) ・ 三角関数の変換 このページのトップへ戻る

あ かまでの角度を求めてください 急いでます 教えてください Clearnote

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

 と求める。上記の直角三角形では である。斜辺の長さを分母、隣辺の長さを分子とする分数の値がコサインの値だ。 直角三角形におけるtan(タンジェント)の値の求め方 最後に、直角三角形において、タンジェントの値を求めていこう。 三角形の辺の長さなどから角度（角の大きさ）を求める方法です。 次の2パターンに分けて説明します。 パターン1：3辺の長さから角度を求める方法 パターン2：2辺の長さと1つの角度から残りの角の大きさを求める方法 メインで活躍する公式は第二余弦定理です。 (第2)余弦定理 ものすごく強力な公式です。 第二余弦定理 については知っているという 150°の内角をもつ三角形 150°三角形とは、 1つの角度が150° の三角形のことです。 ご存じのとおり三角形の面積の求め方は・・・ 三角形面積 ＝ 底辺 × 高さ ÷ 2 ですが、150°三角形の問題は例題のように 高さの情報が無い のが特徴です。

小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

 たて開脚は直角三角形の角度を求める計算を応用する では、縦の開脚角度はどのように求めればよいのでしょうか？ 縦の開脚は少し工夫が必要ですが、横と同じように三角形の公式で求めることができます。 たて開脚の場合に使用する考え方は直角三角形。「三角形の面積 底辺 高さ 」 「 三 角 形 の 面 積 = 底 辺 × 高 さ ÷ 2 」 で求められます。 たとえば、「底辺 9 c m 高さ 6 c m の三角形」の面積は 9 × 6 ÷ 2 = 27 c m 2 となります。 なぜ 底辺 高さ 底 辺 × 高 さ ÷ 2 で求まるのかについては 「三角形の面積の求め方。 なぜ底辺×高さ÷2で求まるのか？ 」 で解説しています。 ② 直角三角形・正三角形の性質を使って求める 「底辺 a 、斜辺 c の直角三角 特別な三角形の場合を除いては 余弦定理とかでは角度自体を求めるのは無理です。 sinA や cosAの値は求められますのでその値から 三角関数表を使って近似値を求める方法です。 例題 Cが直角でAB=5 BC=4 AC=3の三角形の場合 角Bの求め方について説明します。

タンジェントとは何か 中学生でも分かる三角関数の基礎

小５ 算数 小５ ３１ 三角形の角 Youtube

 高校までの範囲ならば、辺の長さが実数で与えられているはずなので特殊な角度だけ覚えておけば大丈夫だと思います。 arctan 0 = 0 arctan 1/√3 = π/6 arctan 1 = π/4 arctan √3 = π/3 （2） 辺cの値を求めます。 直角三角形であるので、 c = √ (a^2 b^2) となります。 cosθ1 = a/c より、 θ1 = arccos a/c となります。 また、 cosθ2 = b/c より θ2 = arccos b/c となります。 (1)とピタゴラスの定理を使用する どのような直角三角形でも、斜辺の長さをc、他の二辺をa、bとしたときに、a 2 b 2 = c 2 が成り立つことがピタゴラスの定理で証明されています。 この定理を利用すると正三角形の高さを求められます。三角比の辺の比率について、下の図を使って説明します。 2つの三角形の左端の角度を見てください。 それぞれの角度は、30度の直角三角形と45度の直角二等辺三角形です。 いろいろある角度の中でこの30度と45度の角度の時は、人が覚えやすい比率になり

正三角形や二等辺三角形の内角 Youtube

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

三角形の内角の性質 三角形の内側にある角のことを 内角 といい、 すべて足すと180° になります。 これは小学生のときに学習しているので覚えている方も多いでしょう。 でも じゃぁ、何で180°になるのか知っていますか？ と言ったら、困ってしまい図のような直角三角形の下側の辺の長さを求めよ。 下側の辺の長さを a とすると、 a × a 3 × 3 = 4 × 4 となります。 計算すると、 a × a 9 = 16 a × a = 16 − 9 = 7 よって、下側の長さは c = 7 となります。 きちんと計算すると、 7 = ⋯ となります。 関連： ルート2、ルート3、ルート5ルート30の値と語呂合わせ 計算ツール 次回は 平行四辺形の3つの性質とその証明 を解説します。三角方程式を解いて角度を求める際は、単位円を用います。 STEP1 角度の範囲を確認する まず、求める の範囲を確認します。 今回は と設定されているので、 単位円 周分を考えます（→ 補足① 単位円と三角比の関係 ）。 STEP2 条件を図示する 与えられた条件を単位円に記入しましょう。 今回は なので、 の直線を引きます。 , , の長さの感覚は、暗記した直角三角形とともに身につけておきましょ

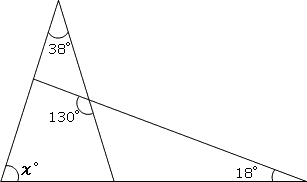
角度の求め方 算数の教え上手 学びの場 Com

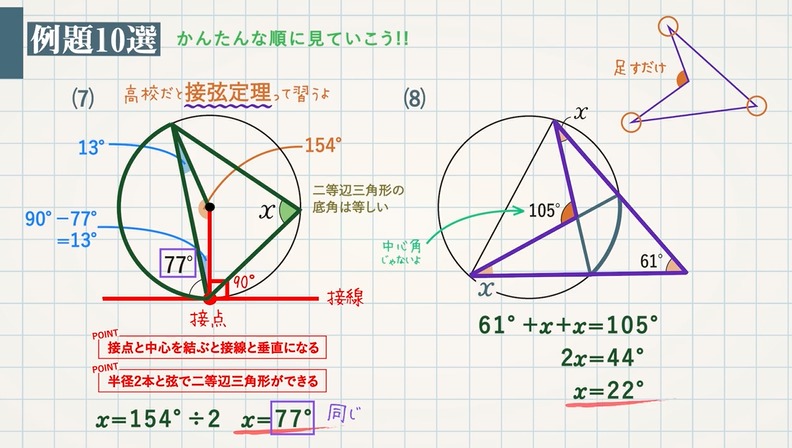
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

 1 三角関数の角度の求め方、三角方程式の解き方 2 三角関数の角度を求めるsin編 21 三角関数の角度sinを求める①：単位円を利用する 22 三角関数の角度sinを求める②：sinθ=aのときy=aをグラフに書く 3 三角関数の角度を求めるcos編 4 三角関数の角度を求めるtan編 5 三角関数の角度を求めるときは、θの範囲を忘れないこと 二等辺三角形の辺の長さの求め方 頂角から底辺に垂線を下ろし、直角三角形を得る （頂角が の場合はそのまま全体を見る） 直角三角形について、 (i) 角度がすべてわかり、しかも有名角（, , , など）である場合 → 直角三角形の辺の比 を利用 (ii) 辺の長さがわかっている場合 → 三平方の定理 を利用 それぞれの詳しい求め方は、例題で解説します。 例題①「直角三角形の辺の比を利用する」小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。

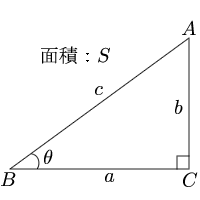
直角三角形 底辺と高さ 三角形の計算 計算サイト

三角形の角度を求める 思考力を鍛える数学

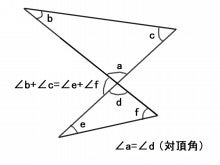
角度の求め方 数学が嫌いなんです

二等辺三角形の角を求める Youtube

中学受験 平面図形 重なった正方形と正三角形から角度を求めるには さんすうがく

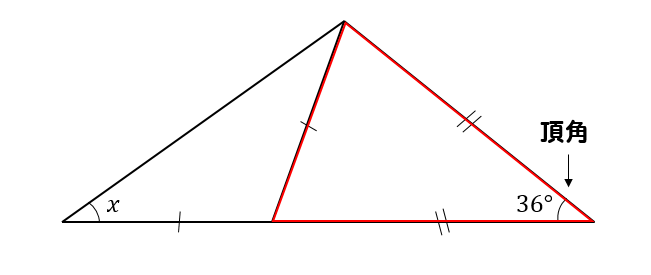
二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ

中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ

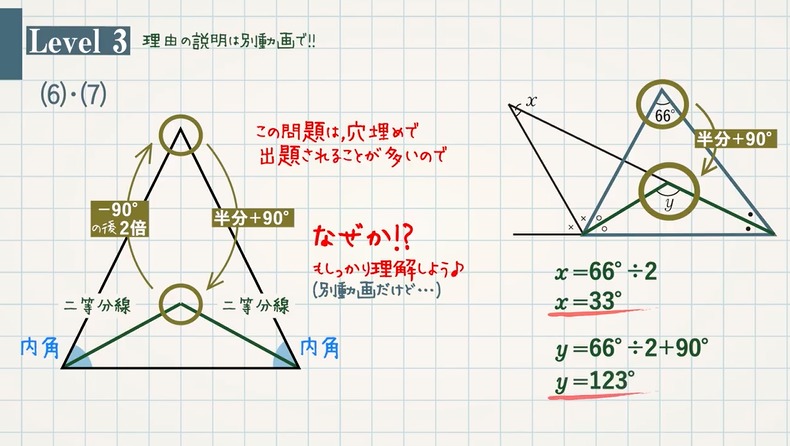
角度の計算 裏技まとめ 教遊者

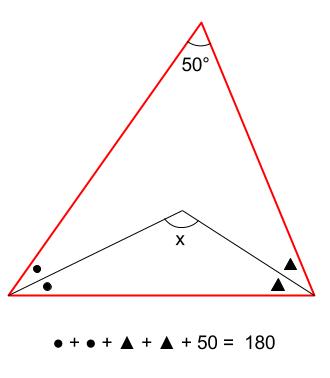
中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su

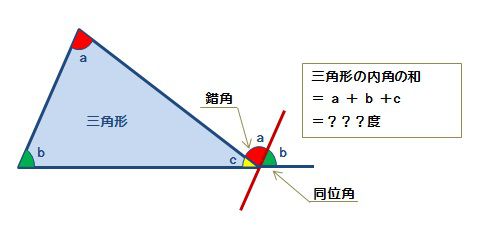
三角形の内角の和 算数の公式覚えてますか

図形の角度を求める問題の解き方 現役塾講師のわかりやすい中学数学の解き方

1

直角三角形の解法 1

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

求め方がわからないです Clearnote

正三角形の定義は 面積公式 高さや重心についても解説 受験辞典

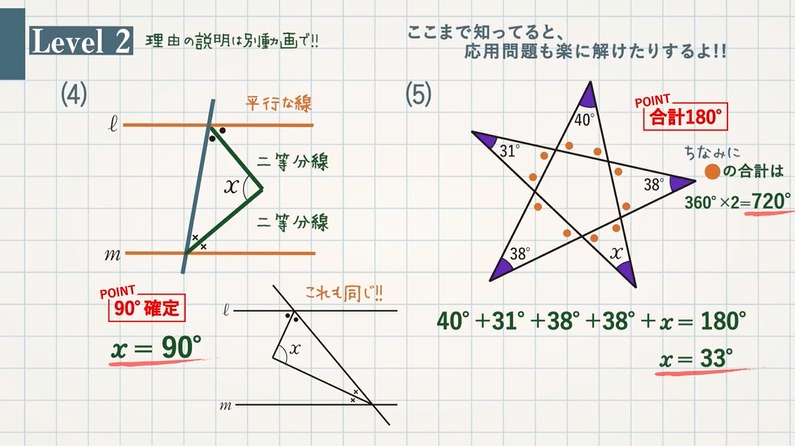
角度の計算 裏技まとめ 教遊者

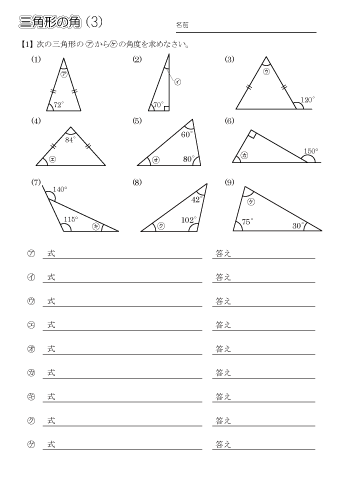
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

余弦定理で角度を求める方法 数学の星

Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算

二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明

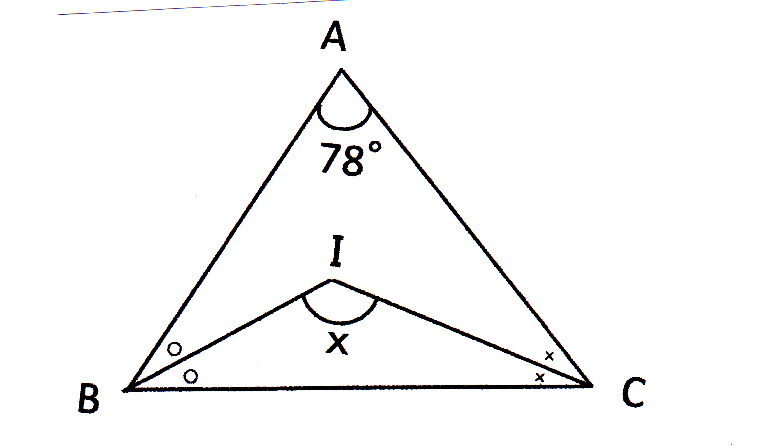
三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方

3

1

二等辺三角形の角度を利用した難問 良問 ラングレー2題 なぜか分かる はかせちゃんの怪しい研究室

二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題

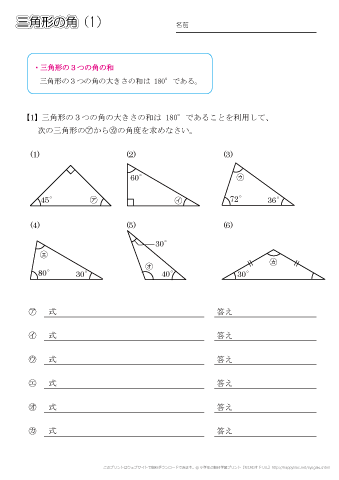
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

三角形の面積公式まとめ 求め方をわかりやすく解説 受験辞典

角度の計算 裏技まとめ 教遊者

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

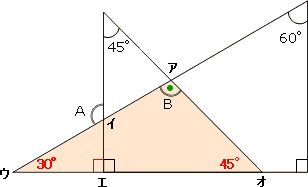
角度の求め方 算数の教え上手 学びの場 Com

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

直角三角形の角度の求め方 教えて下さい 斜辺以外の２辺の長さが分かっ Yahoo 知恵袋

普通の電卓で計算できる直角三角形の近似計算

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

底辺と高さから角度と斜辺を計算 高精度計算サイト

数学 中2 53 角度チャレンジ Lv 1 Youtube

角度の求め方 算数の教え上手 学びの場 Com

三角形の３辺から角度を計算 高精度計算サイト

中2 数学 4 2 三角形の角度の利用 Youtube

直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage

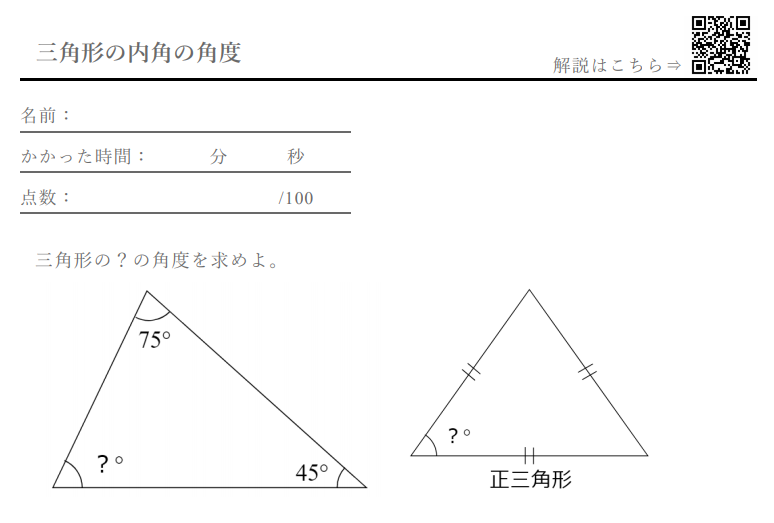
三角形 の内角の角度 計算ドリル 問題集 数学fun

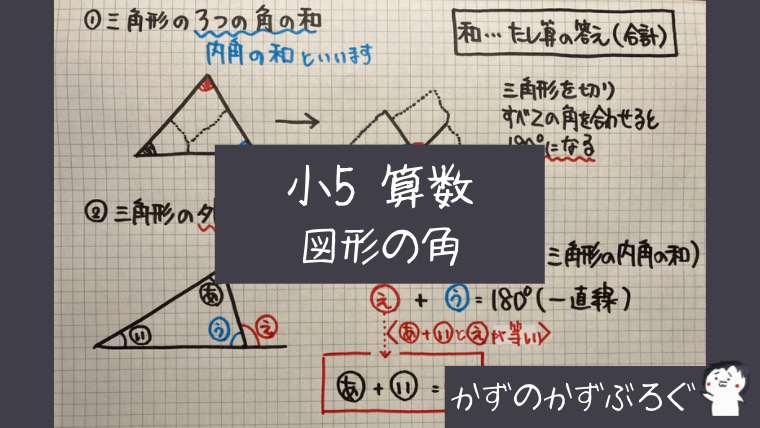
小5算数 図形の角 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ

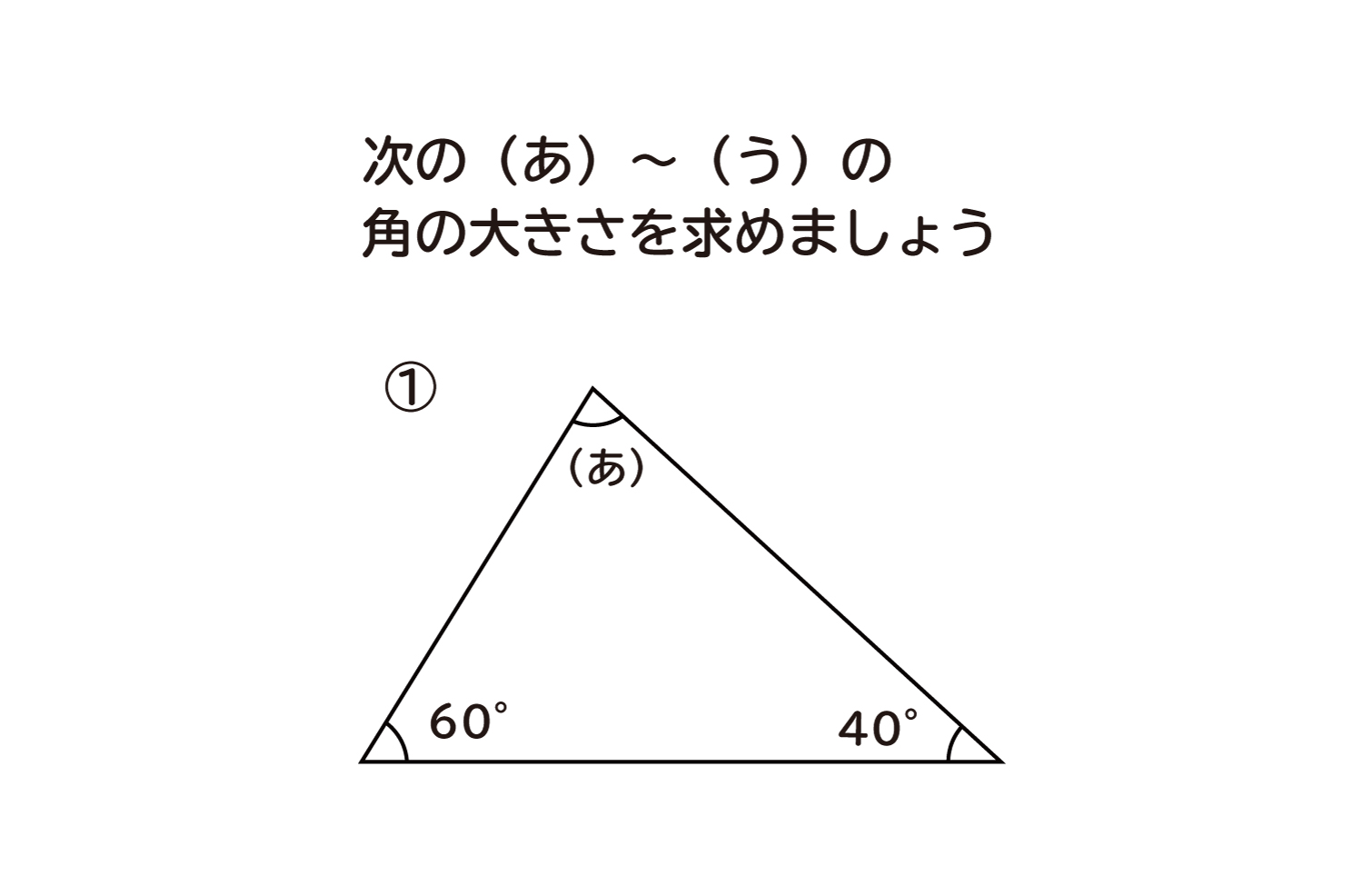
小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル

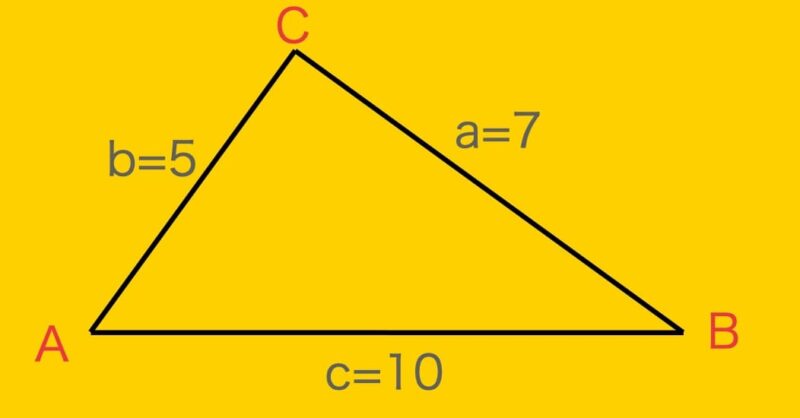
余弦定理 で角度を求める方法２パターン 豊富な例題で理解 トムラボ

円と三角形 角度 中学から数学だいすき

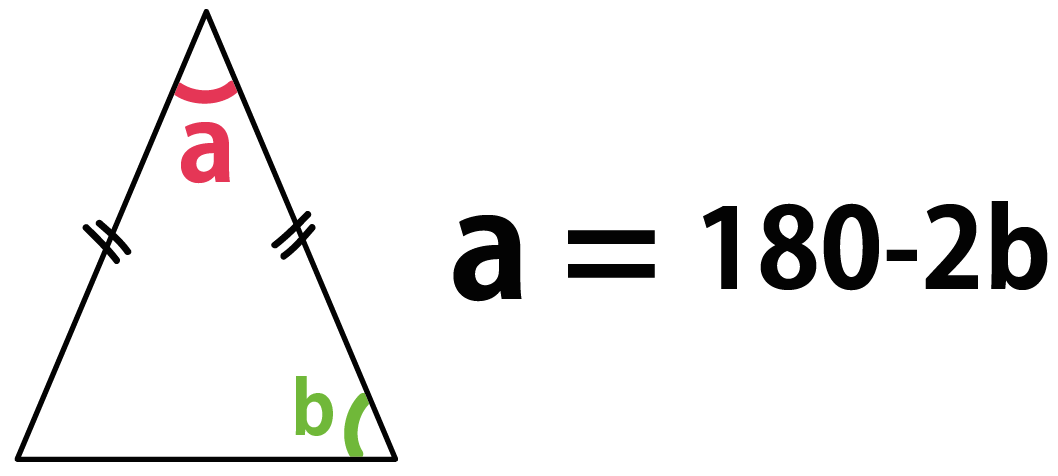
簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

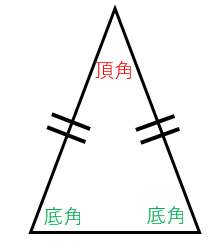
二等辺三角形の角度の求め方と例題 具体例で学ぶ数学

1

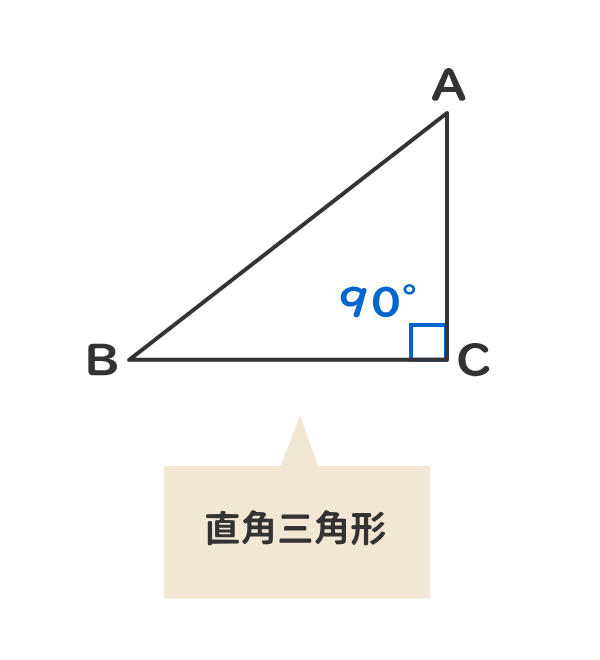
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

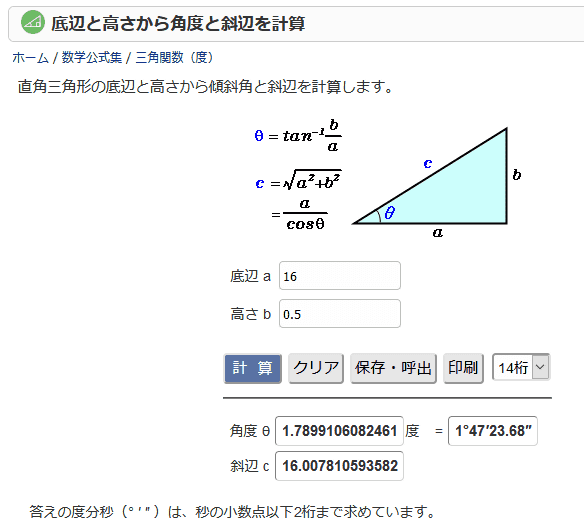
表計算ソフトを使って 底辺 と 高さ から 角度 を求める

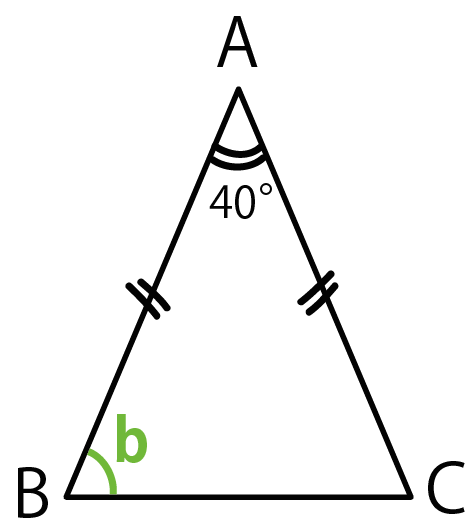
簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

角度の求め方 算数の教え上手 学びの場 Com

二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト

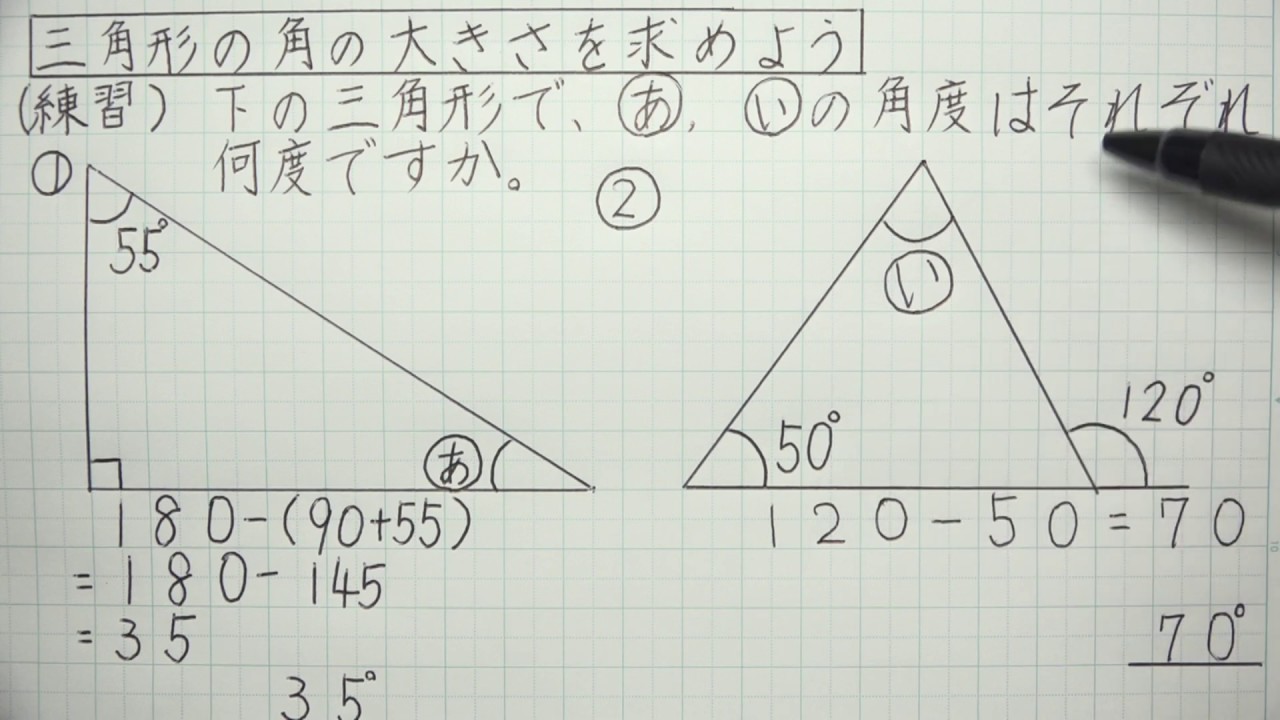
5年算数 図形の角と合同 ６ 三角形の角の大きさを求めよう Youtube

中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット

三角形の性質と角度計算 小学４年生算数 小学生の算数が基礎から子どもは学べ 大人は教えられる算数サイト

正確な角度の測定 割り付け

二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明

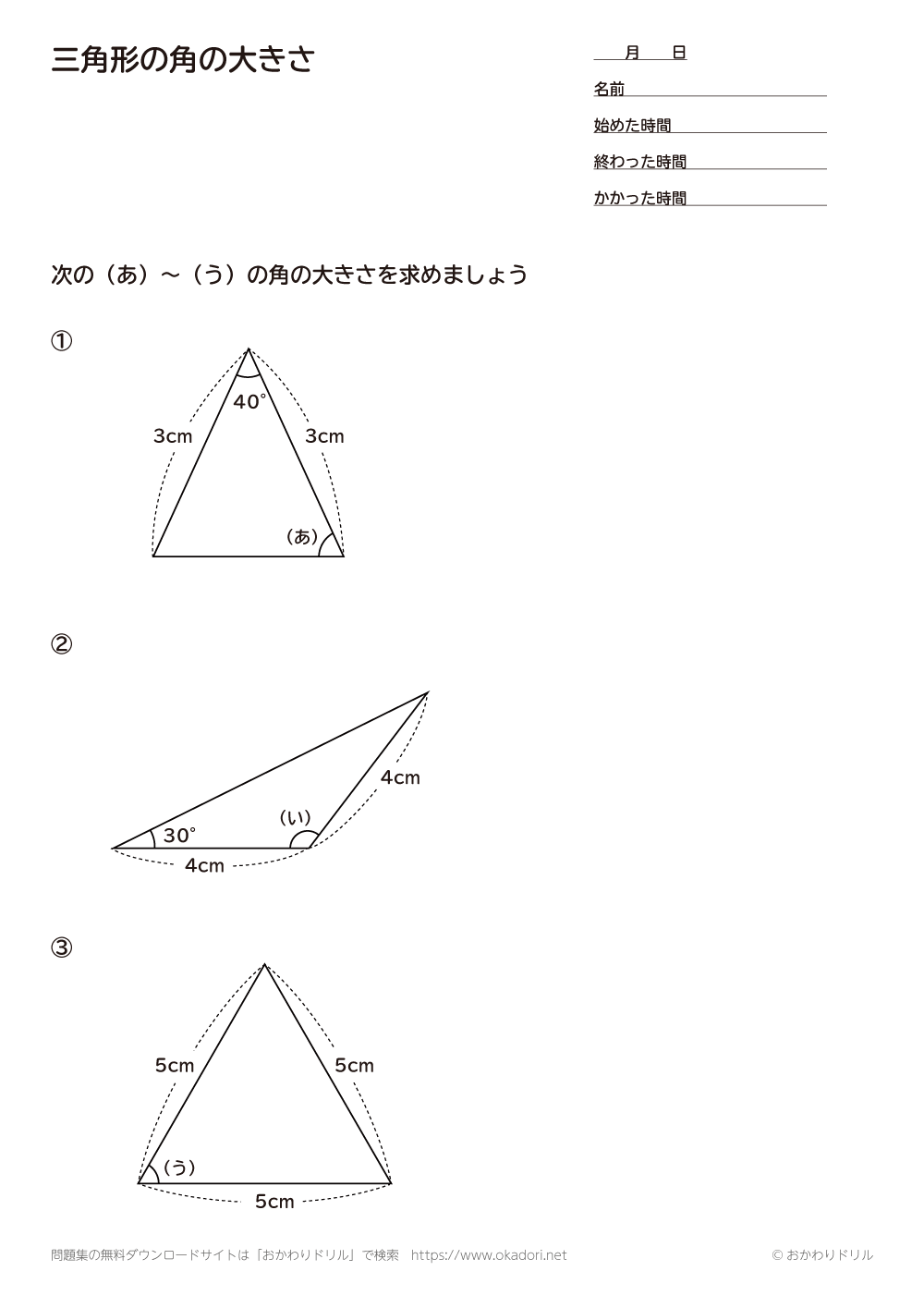
小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル

直角三角形の解法 1

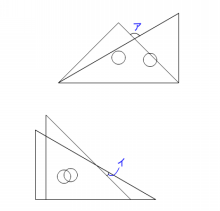
重なり合う三角定規を使った角度の計算問題 小4 小５の算数 きいとこ

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集 Waenavi

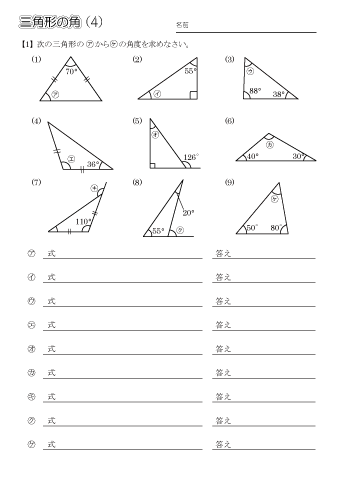
小学５年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生

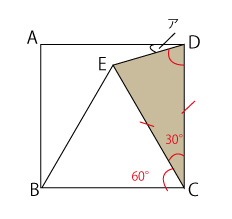
いろいろな角度を求める問題1 図形の等辺を利用する 中学受験準備のための学習ドリル

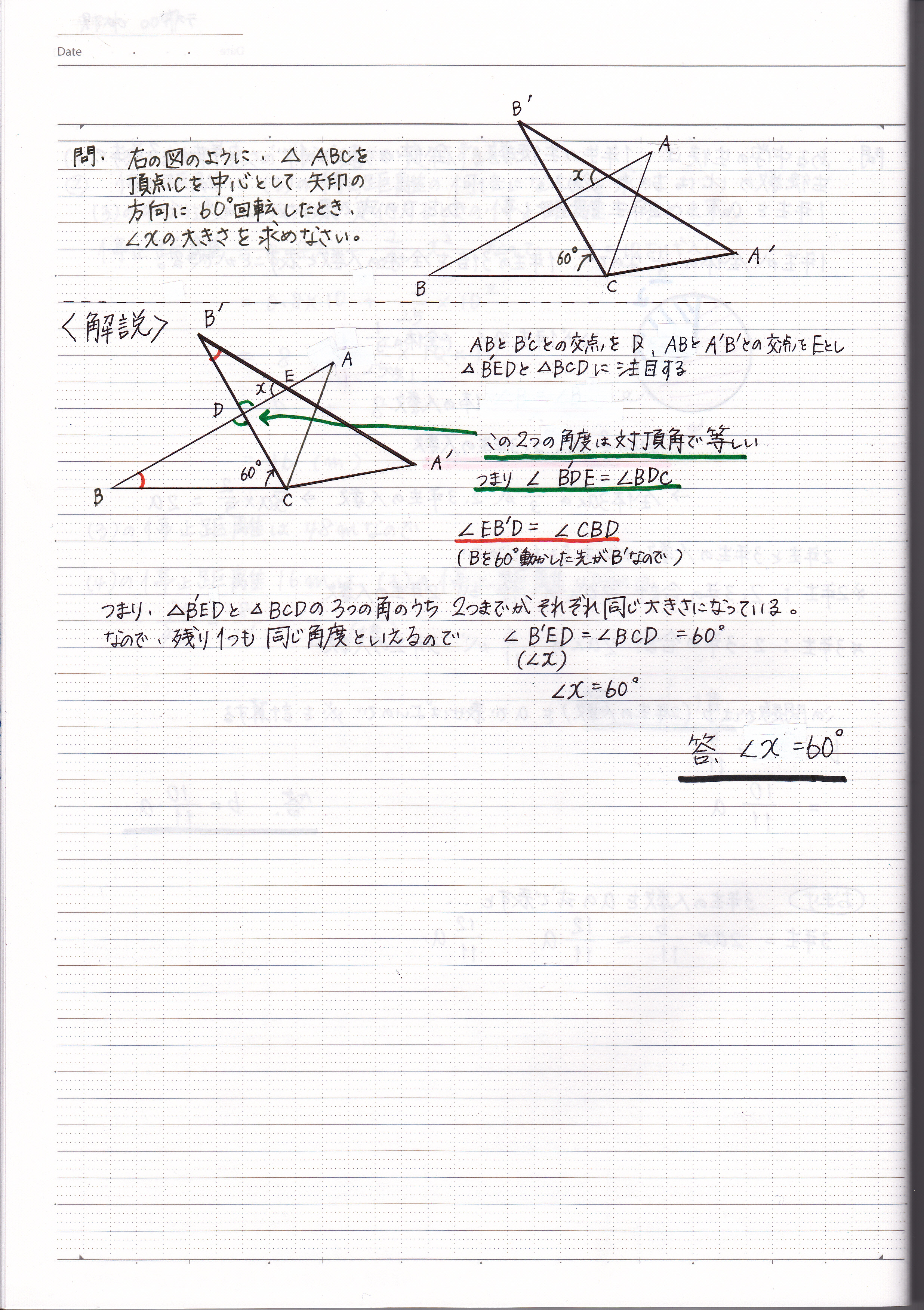
回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方

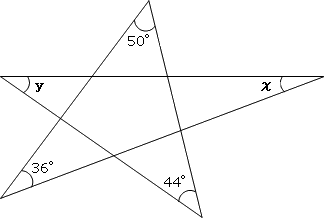
角度の求め方 算数の教え上手 学びの場 Com

三角形の角度を求める問題 小学生 中学生の勉強

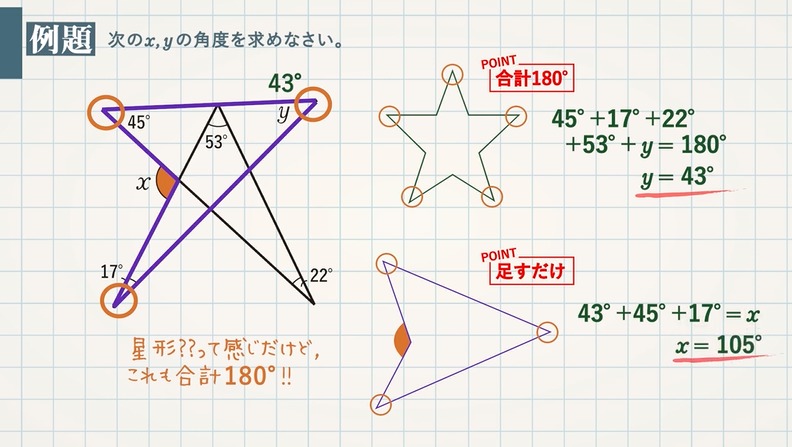
角度の計算 裏技まとめ 教遊者

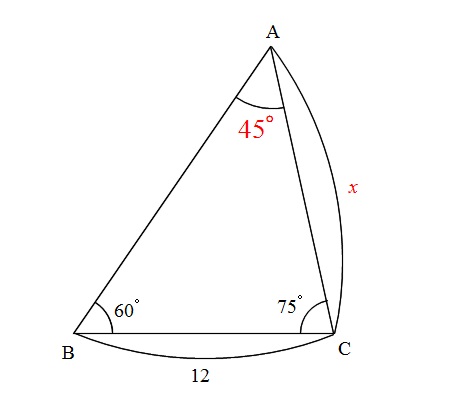
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

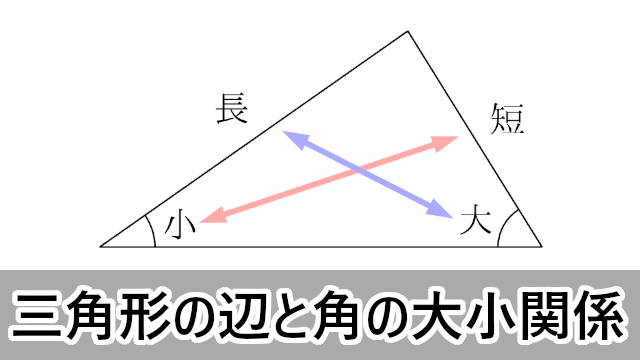
数学ia 三角形の角の大きさと辺の長さの関係 証明 大学入試数学の考え方と解法

二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学

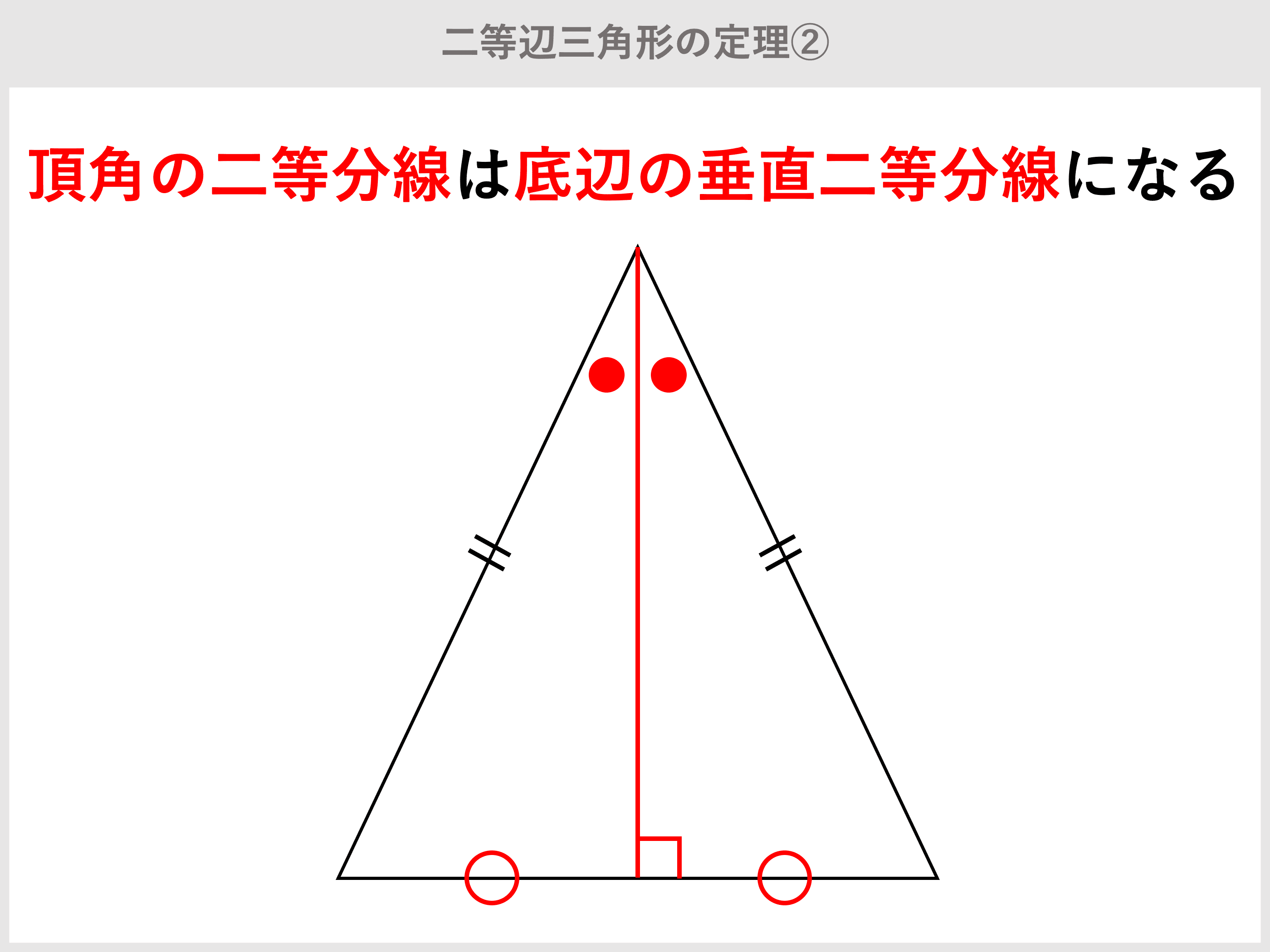
三角角度求め方 Motics

中学受験 平面図形 重なった２つの三角形から角度を求めるには さんすうがく

角度を求める問題 スリッパを探そう 苦手な数学を簡単に

三角関数の角度の求め方と変換公式をわかりやすく解説 受験辞典

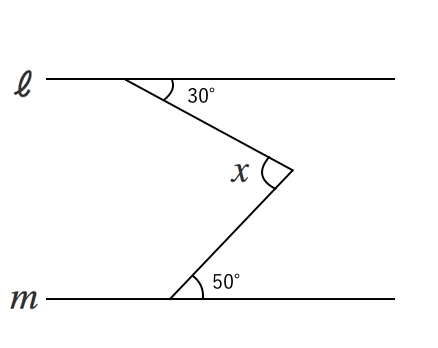
図形の調べ方 角度を求める問題 苦手な数学を簡単に

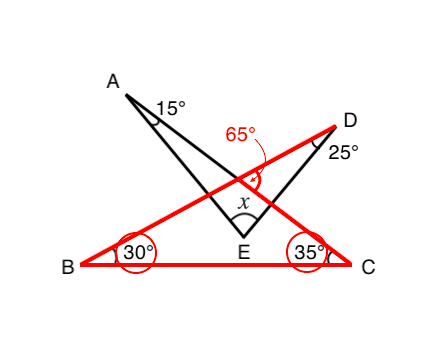
ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく

円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ

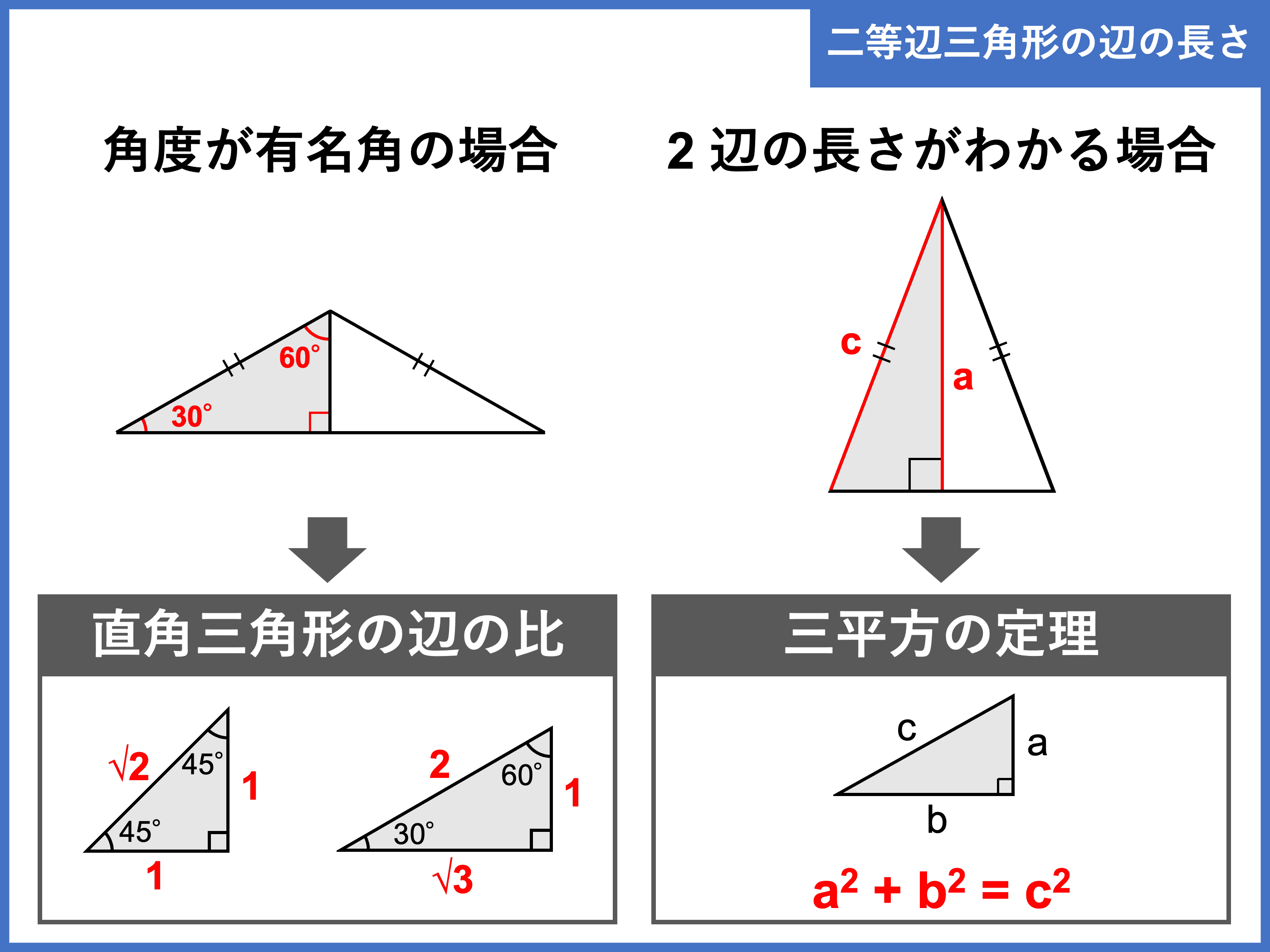
二等辺三角形とは 定義 定理や 角度 辺 面積の求め方 受験辞典

三角形の辺から角度を計算 製品設計知識

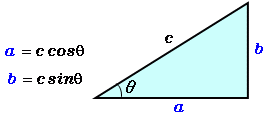
角度と斜辺から底辺と高さを計算 高精度計算サイト

角度の求め方 角度の求め方 Mqttk

中2数学 ブーメラン型角度の求め方を解説 数スタ

三角形の角度を求める問題 小学生 中学生の勉強

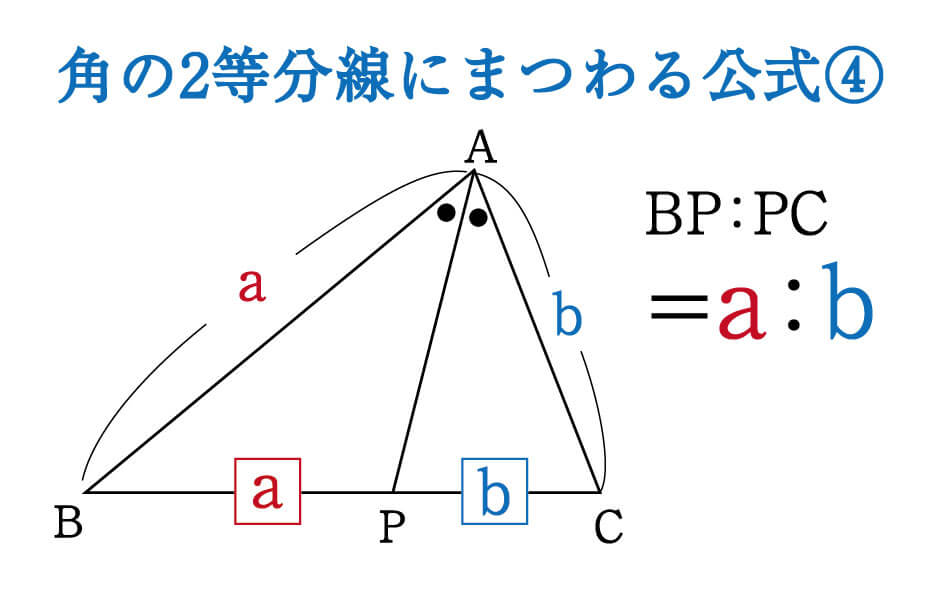
数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

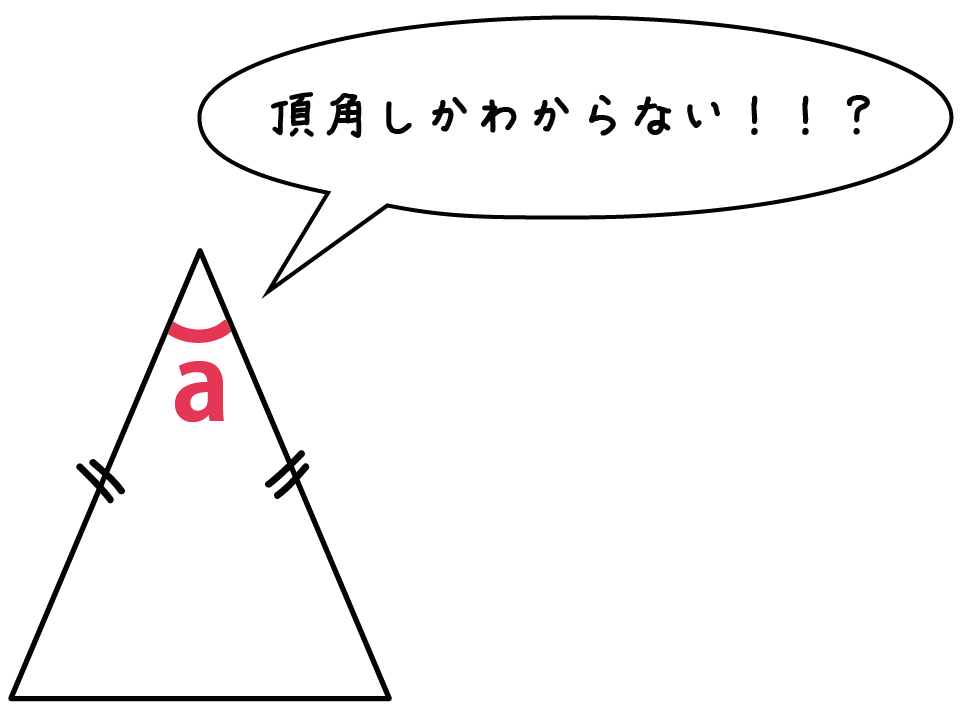
簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく

余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ

図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に